3과목 : 02 통계분석

01.통계 기본 용어 1

- 모집단 : 데이터의 전체 집합
- 모수 : 모집단의 특성을 나타내는 수치들
   - 모집단의 평균(𝝁), 분산(𝝈2) 같은 수치들
- 표본 : 모집단의 개체 수가 많아 전부 조사하기 힘들 때 모집단에서 추출(sampling) 한 것
   - 모집단의 특성을 알기 위해 표본을 추출함 (오차 발생) => 추론(inference)
- 통계량
   - 표본의 특성을 나타내는 수치들
   - 표본의 평균, 분산(s2) 같은 수치를 통계량(statistic)이라고 함

- 모집단에 대해 알고자하는 값을 모수라고 하고, 모수를 추론하기 위해 구하는 표본의 값들을 '통계량' 이라 함

통계량 문제 (22회)

 

02.통계 기초 용어 2

- 표본점
   - 어떤 행위를 했을 때 나올 수 있는 값
   - 주사위 굴리는 행위를 했다면 1, 2, 3, 4, 5, 6 중 하나
- 표본공간
   - 모든 표본점의 집합
   - 주사위 굴리는 행위에 대한 표본공간 S = {1,2,3,4,5,6} 
- 사건
   - 표본점의 특정한 집합
   - 주사위를 한 번 굴렸을 때 홀수가 나오는 사건을 A라고 하면 A = {1, 3, 5}
- 확률
   - 어떤 사건(A)이 발생할 확률은 P(A)와 같이 표기함
   - 확률값 :  0<= P(A) <= 1,  P(S) = 1 

03-01.확률적 표본추출법의 종류

- 단순 무작위추출(simple random sampling)
  - 모집단의 각 개체가 표본으로 선택될 확률이 동일하게 추출되는 경우
  - 모집단의 개체 수 N, 표본 수 n 일 때 개별 개체가 선택될 확률은 n/N 임
- 계통추출(Systematic sampling)
  - 모집단 개체에 1, 2,…,N 이라는 일련번호를 부여한 후,첫 번째 표본을 임의로 선택하고 일정 간격으로 다음 표본을 선택함
- 층화추출법(stratified sampling)
  - 모집단을 먼저 서로 겹치지 않는 여러 개의 층으로 분할한 후, 각 층에서 단순임의추출법에 따라 배정된 표본을 추출하는 방법
- 군집추출(Cluster sampling)  
  - 모집단을 특성에 따라 여러 개의 집단(cluster)로 나눈다
이들 집단 중 몇 개를 선택 한 후, 선택된 집단 내에서 필요한 만큼의 표본을 임으로 선택한다

 

층화추출법을 찾는 문항 (17회)

 

03-02.표본 조사

- 조사과정에서 발생하는 오류는 표본추출 오류와 비표본추출 분류할 수 있다
- 표본편의(Sampling Bias)는 표본추출방법에서 기인하는 오차를 의미한다
- 표본편의는 확률화(Randomization)에 의해 최소화하거나 없앨 수 있다
- 표본오차는 표본크기가 증가함에 따라 감소하지만, 비표본오차는 감소하지 않는다

틀린 설명 고르기 (19회)
- 비표본오차도 표본크기 증가에 따라 감소한다고해서 틀림

 

04.자료의 척도(Scale)

- 명목척도 : 단순히 측정 대상의 특성을 분류하거나 확인하기 위한 목적
   - 남녀, 혈액형, 출생지 등
- 서열(순위)척도 : 항목들 간에 서열이나 순위가 존재하는 척도
   - 서열척도는 대소 또는 높고 낮음 등의 순위만 제공할 뿐 양적인 비교는 할 수 없음
   - 서열척도의 예: 금은동메달, 매우불만족-불만족-보통-만족-매우만족   
- 연속형 자료를 나타내는 척도로 등간척도와 비율척도가 있음
- 등간척도 : 순위를 부여하되 순위 사이의 간격이 동일하여 양적인 비교가 가능함
   - 절대 0점이 존재하지 않음, 온도계 수치, 물가지수
- 비율척도 : 절대 0점이 존재하여 측정값 사이의 비율 계산이 가능한 척도
   - 몸무게, 나이, 형제의 수, 직장까지의 거리

자료의 척도 설명으로 틀린 것 찾기 (19회)
- 구간척도는 아무것도 없는 상태를 0으로 정할 수 있는 척도로 해서 틀림
척도에 대한 설명 중 부적절한 것 찾기 (20회)
- 비율척도 설명 틀림
성별 구분에 사용되는 척도 (명목척도) 찾기 (20회)
매우불만족 ~ 매우만족에 사용되는 척도 (순서척도) 찾기 (20회)
출생지 구분에 사용되는 척도 (명목척도) 찾기 (22회)

 

05.집중화 경향(Central Tendency)

- 평균(Mean) : 값 들의 무게 중심이 어디인지를 나타내는 값, 산술 평균
- 중앙값(Median) : 자료를 크기 순서대로 배열했을 때, 중앙에 위치하게 되는 값
- 최빈값(Mode) : 어떤 값이 가장 많이 관찰되는지 나타낸 값

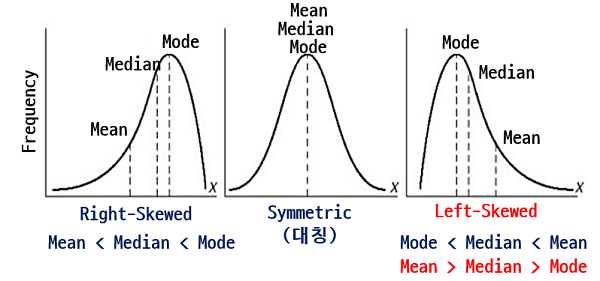
- 평균은 양 꼬리 값의 크기가 변할 때 영향을 크게 받지만 중앙값은 그러한 변화에 영향을 거의 받지 않음

 

평균 > 중앙값, 왼쪽으로 치우쳐진(오른쪽으로 꼬리가 긴) 분포의 평균과 중앙값의 관계 찾는 문제 (21회)

 

06.비모수적 추론(검정)

- 자료가 추출된 모집단의 분포에 대해 아무 제약을 가하지 않고 검정을 실시하는 검정 방법
- 모집단의 특성을 몇 개의 모수로 결정하기 어려우며 수많은 모수가 필요할 수 있음
- 추론에서 계산이 모수적 방법보다 훨씬 단순함
- 관측값들의 순위와 두 관측값 사이의 부호 등을 이용해 검정
> 부호 검정(Sign Test) : 데이터의 순위를 계산하여 중심 위치 모수 보다 작거나 큰 순위에 대한  분포를 이용하는 비모수 검정
- 모수 자체보다 분포 형태에 관한 검정을 실시함
- 관측된 자료가 특정 분포를 따른다고 가정할 경우 이용됨

비모수검정의 특징 아닌 것 찾기 (18회, 23회)
- 평균, 분산을 이용한 검정이라해서 틀림
부호검정 써놓고 부호검정 고르기 (21회)

 

07.통계 검정

- 표본특성이 2개 표본 이상일 때의 비모수 검정
   - 부호검정, 크루스칼-왈리스 검정, 맨-휘트니 검정, 카이스퀘어 독립성 검정
   - 부호검정(Sign-Test) : 데이터의 순위를 계산하여 중심 위치 모수보다 작거나 큰 순위에 대한 분포를 이용하는 비모수 검정
- 단일표본(one sample) 검정
   - 카이스퀘어 검정
- 두 범주형 집단의 평균 차이 검정 방법
  - t-test  

카이제곱 검정을 틀린 것으로 찾는 문제 (17회)
t-test 묻는 문제 (21회)

08.통계적 추정(Estimation)

- 추정 : Estimation, 통계량을 사용하여 모집단의 모수를 구체적으로 추측하는 과정을 말함
- 점추정 : Point estimation, 통계량 하나를 구하고 그것을 가지고 모수를 추정하는 방법
  - 하나의 점으로 값을 표현하는 것
  - 점추정의 예) 통계학 수업을 수강한 전체 학생 중에서 50명을 뽑아 조사한 결과 기말 최종 점수가 80점 이었다면, 50명 뿐 아니라 나머지 통계학을 들은 학생들의 점수도 80점 정도겠구나라고 하는 것
- 구간추정 : Interval estimation, 통계량을 제시하는 것은 같지만 모수가 포함되리라고 기대되는 ‘범위’(=신뢰구간)를 만들어서 추정하는 것으로, 점추정의 정확성을 보완하는 방법이다 (22년 2월 24일 수정)
- 신뢰구간(Confidence interval)  
  - 99%의 신뢰구간이 95%의 신뢰구간보다 길다
  - 관측치의 크기가 커지면 신뢰구간의 길이는 줄어든다
  - 표본크기가 커질수록 신뢰구간이 좁아진다. 이는 정보가 많을수록 추정량이 더 정밀하다는 것을 의미한다
- 신뢰수준(Confidence level) 
  - 모수값이 정해져 있을 때 다수의 신뢰구간 중 모수값을 포함하는 신뢰구간이 존재할 확률
  - 신뢰수준 95% 의미는 실제 모수값이 신뢰구간에 존재할 확률이 95%라 할 수 있다

 

틀린 것 고르기 (17회)
- 신뢰수준 95% 의미는 추정값이 신뢰구간에 존재할 확률이 95%라 할 수 있다 => 틀린 문장
신뢰구간에 대한 설명으로 적절하지 않은 것 (22회)
- 95% 신뢰구간은 미지의 수가 포함되지 않을 확률이 95%를 의미한다

 

 

 

 

09.가설검정

- 가설검정(Statistical hypothesis testing)
   - 모집단에 대한 어떤 가설을 설정한 뒤에 표본관찰을 통해 그 가설의 채택 여부를 결정하는 분석 방법
- 귀무가설(null hypothesis)
   - 가설검정의 대상이 되는 가설, 연구자가 부정하고자 하는 가설
   - 설정한 가설이 진실할 확률이 극히 적어 처음부터 버릴 것(기각)이 예상되는 가설
- 대립가설(anti hypothesis)
   - 귀무가설이 기각될 때 받아들여지는 가설
   - 귀무가설과 달리 실제 검증대상이 안되며, 단순히 귀무가설이 기각될 때 대체되는 가설을 말함
- 기각역
   - 귀무가설을 기각하는 통계량의 영역
   - 귀무가설이 옳다는 전제하에 구한 검정 통계량의 분포에서 확률이 유의 수준인 부분을 말한다.

대립가설 찾기 (21회)

 

10.제1종, 2종 오류

- 제1종 오류(𝜶 error)
   - 귀무가설이 옳은데도 불구하고 이를 기각하게 되는 오류
- 제2종 오류(𝜷 error)
   - 귀무가설이 옳지 않은데도 이를 채택하는 오류

- 두 가지 오류가 작을 수록 바람직함
- 두 가지를 동시에 줄일 수 없기 때문에 1종오류를 범할 확률의 최대 허용치를 미리 어떤 특정한 값(유의수준)으로 지정해 놓고 제 2종 오류의 확률을 가장 작게 해주는 검정 방법을 사용함
- 유의 수준(Significance level)
   - 제 1종 오류의 최대 허용 한계
   - 유의수준 0.05(5%) : 100번 실험에서 1종 오류 범하는 최대 허용 한계가 5번
- 유의 확률(= P-value)
   - Significance probability, 0 ≤ P-Value ≤ 1, 1종 오류를 범할 확률
   - P-Value가 0.05(5%) : 95%의 신뢰도로 귀무가설을 기각한다
   - 귀무 가설이 맞다는 전제하에, 통계값이 실제로 관측된 값 이상일 확률
   - 귀무가설이 사실일 때 기각하는 1종 오류 시 우리가 내린 판정이 잘못되었을 확률

- 추정과 가설검정 내용으로 틀린 것 (18회)
  P-value 설명이 틀린것
- P-value 설명을 적어주고 P-value 찾기 (18회)
- 유의확률(p-value) 값이 미리 정해 놓은 유의수준 값보다 클 경우, 귀무가설을 기각하고, 대립가설의 가정이 옳다고 할 수 있다
  => 틀려 틀려  (23회)

 

11.확률분포

- 분포 : 일벙한 범위 안에 흩어져 퍼져 있는 정도
- 확률분포 : 확률의 흩어짐을 표현하기 위한 함수, 확률이 확률변수에 따라 흩여져 있는 것을 표현함
- 이산형 확률분포(Discrete)
   - 확률변수가 몇 개의 한정된 가능한 값을 가지는 분포
   - 각 사건은 서로 독립이어야 함(한 사건의 발생이 다른 사건 발생확률에 영향을 주지 않아야 함)
   - 베르누이분포, 이항분포, 포아송분포, 기하분포 등이 있음
- 연속형 확률분포(Continuous)
   - 확률변수의 가능한 값이 무한 개이며 사실상 셀 수 없을 때

12.이산형 확률분포의 종류

- 이항분포 
   - 연속된 n번의 독립적 시행에서 각 시행이 확률 p를 가질 때의 이산 확률 분포
   - n=1일 때 이항 분포가 베르누이분포임
- 베르누이분포
   - 실험 결과 두 가지 중의 하나로 나오는 시행의 결과를 0 또는 1 값으로 대응시키는 확률변수 X에 대해 아래 식을 만족하는 확률변수 X가 따르는 확률분포
   >

   - 모수(=확률변수)가 하나이며 서로 반복되는 사건이 일어나는 실험을 반복적 실행을 확률분포로 나타낸 것

- 포아송분포
   - 단위시간이나 단위공간에서 어떤 사건의 출현횟수가 갖는 분포 (단답형)
   - 특정 기간 동안 사건(events) 발생의 확률을 구할 때 쓰임
   - 일주일간 특정 지역 내에서 일어나는 교통사고의 횟수
   - 보험회사에 가입된 20만명 가운데 심장병으로 1년 동안 5명 이상 사망확률

- 기하분포
   - 베르누이 시행에서 처음 성공까지 시도한 횟수 X의 분포
   - 베르누이 시행에서 처음 성공할 때까지 실패한 횟수 Y=X-1의 분포 

베르누이분포 고르기 (21회)
포아송분포 단답형 (22회)

 

13.기댓값

- 확률변수 X의 가능한 모든 값들의 가중 평균
- 이산적 확률변수 기댓값 : E(X) = ∑x·f(x)
- 연속적 확률변수 기댓값 : E(X) = ∫x·f(x)
- 주사위 1개를 반복해서 던질 때 나타나는 기댓값
> = 1(1/6) + 2(1/6) + 3(1/6) + 4(1/6) + 5(1/6) + 6(1/6)
= 3.5  

이산형 확률변수의 기댓값 계산식 (19회)
주사위 1개 반복 던졌을 때의 기댓값 (22회)

 

14.조건부 확률 (Conditional Probability)

- 사건 B가 발생했다는 조건 아래서 사건 A가 발생할 조건부 확률
- P(A|B) = P(A∩B) / P(B), 단 P(B) > 0
- 두 사건 A, B가 독립사건인 경우 : P(A|B) = P(A), P(B|A) = P(B)
- 독립사건 : A의 발생이 B가 발생할 확률을 바꾸지 않는 사건

- P(음주|사고)는 얼마인가?
- = (음주사고) / (음주사고 + 비음주사고) = 0.07 / 0.13 = 0.54

독립일때의 조건부확률 - 20회
음주, 비음주 사고와 비사고 확률 계산 - 20회

 

15.겨자 사용자가 케찹을 사용할 확률

- 햄버거집에서는 고객들의 취향을 조사한 결과 75%는 겨자를 사용하고, 80%는 케찹을 사용하며, 65%는 이들 두 가지를 사용한다는 사실을 발견했다. 
- 겨자 사용자가 케찹을 사용할 확률은?
- 사상A : 고객은 겨자를 사용한다, 사상B : 고객은 케찹을 사용한다
> P(A|B) = P(A∩B) / P(A) = (둘 다 사용하는 사용자) / (겨자 사용자) = 0.65 / 0.75 = 0.87

확률구하기 문제 (22회)

 

16.확률값, 배반사건, 독립사건

- 모든 사건의 E의 확률 값은 0과 1사이에 있다
- 배반사건 : 교집합이 공집합인 사건들을 말한다
- 독립사건 : A의 발생이 B가 발생할 확률을 바꾸지 않는 사건, 두 사건 A, B가 독립이면 P(B|A)=P(B) 가 성립한다

표본공간, 확률에 대한 부적절한 설명 (19회)
- 독립하는 두 사건 A, B가 독립이면 P(B|A)!=P(B) 성립이라해서 틀림

 

17.계산 문제들

- 동전 3개를 동시에 던져서 앞면이 한 번 나올 확률은?
> 3/8 

 

동전 확률 (23회)

 

18.회귀 분석

- 일반 선형회귀는 종속변수가 연속형 변수일 때 가능하다
- 회귀분석의 모형 검정은 F-test, P-test이다
- 로지스틱 회귀분석의 모형 탐색 방법은 최대우도법이다
- 표본회귀선의 유의성 검정은 두 변수 사이에 선형관계가 성립하는지 검정하는 것으로 회귀식의 기울기 계수 𝜷 =0 일 때 귀무가설, 𝜷≠ 0일 때 대립가설로 설정한다

회귀분석 설명 중 틀린 것 찾기(18회)
- 귀무가설, 대립가설을 반대로 설명(기울기0, 귀무가설임)

 

19.회귀 모형

- 용어 정리
  - 잔차(오차항) : 계산에 의해 얻어진 이론값과 실제 관측이나 측정에 의해 얻어진 값의 차이
  - 독립변수 : 다른 변수에 영향을 받지 않고 독립적으로 변화하는 수
입력 값이나 원인을 나타내는 변수, y = f(x) 에서 x에 해당하는 것
  - 종속변수 : 독립변수의 영향을 받아 값이 변화하는 수
결과물이나 효과를 나타내는 변수 , y = f(x) 에서 y에 해당하는 것
- 회귀모형에 대한 가정
   - 선형성 : 독립변수의 변화에 따라 종속변수도 변화하는 선형(linear) 모형이다
   - 독립성 : 잔차와 독립변수의 값이 관련되어 있지 않다 (Durbin-Watson 검정으로 확인가능)
   - 등분산성 : 잔차항들의 분포는 동일한 분산을 갖는다
   - 비상관성 : 잔차들끼리 상관이 없어야 한다
   - 정상성 : 잔차항이 정규분포를 이뤄야 한다

19-2. 데이터 정규성 확인 방법

- Shapiro-Wilks test
- Q-Q plot
- histogram
- Anderson Darling test
- Kolmogorov- Smirnov test

아닌 것 고르기 (18회)
- Durbin-Watson :회귀 모형에 대한 가정의 독립성 검정에 사용되는 방법

잔차항이 정규분포를 이뤄야 한다 주관식 (20회)
정상성 주관식 (21회)

 

20.다중 회귀모형의 변수 선택법

- 후진제거법(Backward Elimination)
   - 모든 변수가 포함된 모델에서 기준 통계치에 가장 도움이 되지 않는 변수를 하나씩 제거하는 방법
- 전진선택법(Forward Selection)
   - 절편만 있는 모델에서 기준 통계치를 가장 많이 개선시키는 변수를 차례로 추가하는 방법
- 단계적 선택법(Stepwise method)
   - 전진선택법에 의해 변수를 추가하면서 새롭게 추가된 변수에 기안해 기존 변수가 그 중요도가 약화되면 해당 변수를 제거하는 등 단계별로 추가 또는 제거되는 변수의 여부를 검토해 더 이상 없을 때 중단함

변수 선택법 아닌 것 고르기 (18회)
후진 제거법 단답형 문항 (19회)

 

21.다중 회귀모형

- 다중공선성(Multicollinearity)
   - 모형의 일부 예측 변수가 다른 예측 변수와 상관되어 있을 때 발생하는 조건이다. 중대한 다중공선성은 회귀계수의 분산을 증가시켜 불안정하고 해석하기 어렵게 만들기 때문에 문제가 된다.   
- 다중 회귀모형 해석
  - 모형이 통계적으로 유의미한지 확인하는 방법 : F 통계량, 유의확률(P-Value)
  - 회귀계수들이 유의미한가? : 회귀계수의 t값, 유의확률(P-Value)
  - 모형이 얼마나 설명력을 갖는가? : 결정계수 확인
  - 모형이 데이터를 잘 적합하고 있는가? : 잔차통계량 확인, 회귀진단 진행
- 결정계수
  - 결정계수는 전체 분산 중 모델에 의해 설명되는 분산의 양
  > 결정계수 = 회귀제곱합 / 총제곱합
  > 19회 30번 풀자
  - 결정계수가 커질수록 회귀방정식의 설명력이 높아짐
  - 결정계수는 0~1 사이의 범위를 갖음
  - 회귀계수의 유의성 검증은 t값과 p값을 통해 확인  

다중공선성 찾기 (22회)
F통계량 묻는 문항 (19회)
결정계수의 설명으로 부적절 (18회)
- 총변동과 오차에 대한 변동 비율이라해서 틀림

 

22.Lasso 회귀분석

- 회귀계수의 절댓값이 클수록 패널티를 부여한다
- 독립변수가 많아질수록 training data의 설명력은 좋아지지만 과적합 문제가 발생할 수 있다
- 람다값으로 penalty 정도를 조정한다
   - 람다값이(lambda) 너무 크면 모든 항들에 대해 너무 많이 penalty가 적용되므로 model에 데이터를 잘 설명하지 못하는 underfitting 문제가 발생할 것이다
- Lasso regression은 L1 norm을 사용해 패널티를 주는 방식이다
- 자동으로 변수선택을 하는 효과가 있다

L2 norm  이라고 해서 틀린 예가 있었음 (16회, 23회)
- L2 norm 은 릿지회귀!

 

23.상관분석

- 상관계수는 두 변수의 관련성의 정도를 의미한다.
- 피어슨 상관계수는 두 변수간의 선형적인 크기만 측정 가능
- 스피어만 상관계수는 두 변수간의 비선형적인 관계도 나타낼 수 있음
- Cor.test() 함수를 사용해 상관계수 검정을 수행하고, 유의성검정을 판단할 수 있음
- 이때 귀무가설은 '상관계수가 0이다'. 대립가설은 '상관계수가 0이 아니다'
- 공분산이 0이면 관측값들이 4면에 균일하게 분포되어 있다고 추정할 수 있다.

잘못된 설명 찾기(18회 2문제)
- 선형 회귀에 대한 설명 : 종속변수 값을 예측하는 선형모형 추출 방법이다
- tv 광고와 매출액의 상관관계가 크면 당연히 인과관계도 있다고 할 수 있다. (NO!)

 

24.공분산 행렬, 상관행렬

- 주성분 분석의 문제는 척도에 영향을 받는다는 것이다
- 변수들의 선형결합을 유도할 때 분산을 이용하기 때문에 결과적으로 공분산행렬을 이용한 분석의 경우 변수들의 측정 단위에 민감하다
- 공분산 행렬 (covariance matrix) 은 변수의 특정단위를 그대로 반영한 것이고,상관행렬은 모든 변수의 측정단위를 표준화한 것이다
- 설문조사처럼 모든 변수들이 같은 수준으로 점수화 된 경우 공분산행렬을 사용
변수들의 scale이 서로 많이 다른 경우에는 상관계수행렬(correlation matrix)을 사용한다

주성분 분석 설명 중 적절하지 않은 것 (19회, 20회)

 

25.상관분석 해석

이 데이터 프레임은 5개의 변수를 포함한다
Sales와 Price 변수 간 -0.44 정도로 약한 음의 관계이다  (틀린 설명으로 기출 19회)
Education과 Income 변수 간 상관계수는 약 -0.06이다
상관계수의 가설검정은 cor.test()함수를 사용한다

상관계수는 통계적 유의성 판단에 사용하지 못한다! (23회)
- 상관계수는 통계적으로 유의하다 라고 하면 틀린 내용임

 

26.스피어만 상관계수

- 대상자료는 서열척도 사용
- 스피어만 상관계수는 두 변수 간의 비선형적인 관계를 나타낼 수 있다
- 연속형 외에 이산형도 가능하다
- 관계가 랜덤이거나 존재하지 않을 경우 상관 계수 모두 0에 가깝다
- 스피어만 상관 계수는 원시 데이터가 아니라 각 변수에 대해 순위를 매긴 값을 기반으로 한다
- 예) 국어 성적 석차와 영어 성적 석차의 상관계수

틀린 것 찾기 - 두 변수간 비선형적인 관계를 나타낼 수 없다함 (17회)
비선형적인 관계를 파악할 수 있는 상관계수 (21회)
스피어만 - 순위 - 서열척도 (23회)

 

27.피어슨 상관계수 구하기

- 등간척도, 비율척도 사용
- 피어슨 상관계수는 두 변수 간의 선형적인 크기만 측정 가능
- 피어슨 상관계수 = cov(X,Y) / (X의 표준편차X * Y의 표준편차)
>  응답자1의 표준편차 2, 응답자2의 표준편차 2, 두 응답자의 공분산 값 4 이면
>     피어슨 상관계수 = 4 / (2 * 2) = 1
- 피어슨 상관계수에서 두 변수의 상관관계가 존재하지 않을 경우 상관계수는 '0'이다
- 예) 국어 점수와 영어 점수와의 상관계수

피어슨 상관계수 구하기 (22회)
피어슨 상관계수 0의 의미 (22회)

 

28.주성분분석(PCA, Principal Component Analysis)

- 분석할 때 변수의 개수가 많다고 모두 활용하는 것이 꼭 좋은 것은 아니다
- 오히려 변수가 다중공선성이 있을 경우 분석 결과에 영향을 줄 수도 있음
- PCA는 데이터에서 주성분 벡터를 찾아서 데이터의 차원(dimension)을 축소시킴
- 상관관계가 있는 변수들을 결합해 상관관계가 없는 변수로 분산을 극대화하는 변수로 선형결합을 해 변수를 축약하는데 사용하는 방법
- 동일한 주성분은 선형결합으로 이루어져 있다
- 독립변수들과 주성분과의 거리인 '정보손실량'을 최소화하거나 분산을 최대화한다

29.주성분분석의 해석 1

- summary(iris.pca) # pca의 요약정보
- Standard deviation(표준편차) : 자료의 산포도를 나타내는 수치로, 분산의 양의 제곱근으로 정의되며, 표준편차가 작을수록 평균값에서 변량들의 거리가 가깝다.
- Proportion of Variance(분산비율) : 각 분산이 전체 분산에서 차지하는 비중
- Cumulative Proportion(누적비율) : 분산의 누적 비율
- 위의 그림에서
  - 첫 번째 주성분분석 하나가 전체 분산의 62%를 설명하고 있다.
  - 두 번째는 24.7%를 설명하고 있다
  - 반대로 이야기 하면 첫 번째 주성분부분만 수용했을 때 정보 손실은 (100-62) = 38%가 된다
  - 2개의 주성분을 사용하면 전체 분산의 몇 퍼센트를 설명할 수 있는가? 86.75%
  - 주성분 그림에서 주성분 3개를 수용했을 때 잃는 정보량은 얼마인가? 4.3%

2개의 주성분을 사용하면 전체 분산의 몇 퍼센트를 설명할 수 있는가? 86.75% (21회)
80% 이상 자료를 설명하려면 몇 개 주성분이 필요한가 (23회)

 

30.주성분분석의 해석 2

- 아래의 두가지의 결과는 거의 차이가 없다
   - data_1 <-prcomp(data, scale=TRUE)
   - princomp(data, cor=True) 
- 변수들의 scale이 많이 다른 경우 특정 변수가 전체적인 경향을 좌우하기 때문에 상관계수 행렬을 사용하여 분석하는 것이 좋다

- Cumulative Proportion 확인 : 80% 이상 설명하려면 주성분 4개이상 선택하면 된다
- Proportion of variance 확인 : 제 1성분의 설명력은 45%이다
- princomp의 옵션 확인 : cor= TRUE이므로 상관행렬을 활용한 결과이다
- 1차원에서 2차원으로 줄이면 데이터 손실율은 약 30.51%이다

공분산 행렬을 사용했다해서 틀림(19회)
princomp(data, cor=TRUE)와 같은 결과 (19회)

 

- 두 번째 주성분의 함수식은 -0.69*x1 + -0.54*x2 + 0.35*x3 + 0.33 * x4 이다
- 주성분 2개의 누적 기여율은 92.9%이다.
- 변수들의 scale이 많은 다른 경우 특정 변수가 전체적인 경향을 좌우하기 때문에 상관계수 행렬을 사용하여 분석하는 것이 좋다.

 

- scale = TRUE 이므로 상관행렬을 사용한 것이다.
(20회)

 

31.시계열 

- 시계열 자료 : 시간의 흐름에 따라 관측된 데이터
- 시계열 자료의 정상성(Stationary)
   - 모든 시점에 대해 일정한 평균을 갖는다
   - 모든 시점에 대해 일정한 분산을 갖는다
   - 공분산은 단지 시차에만 의존하고 시점 자체에는 의존하지 않는다
- 정상시계열로 전환
   - 평균이나 분산이 일정하지 않은 자료(비정상시계열 자료)에 대해서는 변환을 통해 정상시계열로 바꿀 수 있다
   - 비정상시계열 자료는 정상성을 만족하도록 데이터를 정상시계열로 만든 후 시계열 분석을 수행한다  
   - 분산이 일정하지 않은 경우에는 원계열에 자연로그(변환)을 취하면 정상시계열이 된다. 
   - 차분 : 비정상시계열을 정상시계열로 전환하는 방법 중 현 시점의 자료값에서 전 시점의 자료값을 빼주는 것 의미함

시계열 자료를 고르는 객관식 (16회)
정상성(정상시계열) 주관식 (16회)
차분 주관식 문제 (18회, 23회)
시계열 자료의 정상성 (22회)
- 틀린 것 찾기 : 모든 분산이 시점에 의존하지 않는다. => 공분산에 대한 것임
정상시계열 설명으로 틀린 것 (23회)
- 차분 설명 틀림 (비정상을 정상으로 만들때 사용되는 것이 차분)

 

32.시계열 모형

- 자기회귀(AR) 모형 : 현시점의 시계열 자료에 과거 1시점 이전의 자료만 영향을 준다면 이를 1차 자기회귀모형이라고 하며 AR 모형이라 한다
- 이동평균(MA) 모형 : 현시점의 자료를 유한 개의 백색잡음의 선형결합으로 표현되었기 때문에 항상 정상성을 만족한다. 자기상관함수 p+1시차 이후 절단된 형태를 취한다
- ARIMA(자기회귀누적이동평균모형) :
   - 대부분의 많은 시계열 자료가 자기회귀 누적이동평균모형을 따른다
   - 기본적으로 비정상 시계열 모형이기 때문에 차분이나 변환을 통해 AR, ARMA, MA 모형으로 정상화할 수 있다
   - ARIMA(1, 2, 3)에서 AR로는 1번 차분, ARMA로는 2번 차분, MA로는 3번 차분하여 정상화 한다 

이동평균모형 주관식 문항 (19회)
차분 횟수 (22회)
- ARIMA(AR, ARMA, MA) 

 

33.분해 시계열

- 시계열에 영향을 주는 일반적인 요인을 시계열에서 분리해 분석하는 방법
1.   추세요인 : 자료의 그림을 그렸을 때 그 형태가 오르거나 내리는 등 자료가 어떤 특정한 형태를 취할 때
2.   계절요인 : 고정된 주기에 따라 자료가 변화하는 경우
3.   순환요인 : 물가상승률, 급격한 인구 증가 등의 이유로 알려지지 않은 주기를 가지고 자료가 변화하는 경우
4.   불규칙요인 : 위 세 가지 요인으로 설명할 수 없는 회귀분석에서 오차에 해당하는 요인에 의해 발생

순환요인을 주기를 가지고 변화하는 자료로 ...  (16회)
분해 시계열 주관식 문항 (17회)
시계열 분해요인이 아닌 것 찾기 (19회)
- 추세요인, 계절요인, 순환요인이 있음
분해시계열 요인이 아닌 것 (23회)
- 정상요인은 아님!!

 

34.교차분석(Cross Tabulation)

- 두 변수 간의 연간 관계를 볼 때 교차표를 작성하여 변수들 간 관계를 분석하게 됨
- 교차 분석에 사용되는 검정 통계량이 카이스퀘어 분포를 다루기 때문에 카이스퀘어 검정이라 함
- 교차 분석은 두 변수 부류가 범주형이어야 함
- 교차표로 두 변수의 값이 공유하고 있는 빈도수가 몇 개인지 파악할 수 있음

올바르지 않은 것 고르기 (17회)
- 범주형 변수가 아니어도 사용이라고 했음

 

35.사회연결망 분석

- 2차원 모드 : 사회연결망 분석에서 행과 열에 다른 개체가 배열되는 매트릭스
- 근접중심성 : 사회연결망 분석에서 간접적으로 연결된 모든 노드 간 거리를 합산해 중심성 측정하는 방법

2차원 모드, 근접중심성 찾는 문제 각각 있었음 객관식으로! (17회)